昨天物理考试答题居然发生重大答题事故，最后4道大题漏了第一道大题，然后把第二题写在答题纸的第一题位置上，最后全部写完后才发现问题所在，还剩二十分钟问老师还有没有答题纸，也没有要到。。。最后4大题答案就全部错开答了，估计要挂了。太不应该了，当然有了这次教训后也未必是坏事，以后就涨记性了。
今天化学生物希望能稳住，加油👏
分类目录归档：学习知识
通用技术实践课
为期两天的通用技术实践课一如既往地在少年宫开展，不用上学就是开心😄
四校联考
还有一个多星期就要和高三一起参加四校联考。
苏州，常州，盐城，扬州中学。👏加油鸭
合格性考试
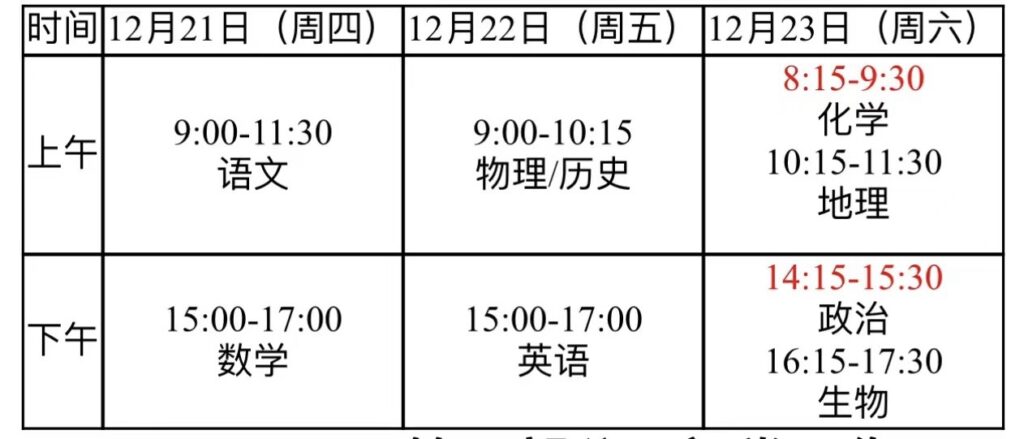
今天已经开始合格性考试啦！时间过的真快。
还记得当年音乐考试，问唢呐的音色特点？实在是不会，于是直接写了：曲儿小，腔儿大。😄
零点的定义
零点的定义
- 1.定义：零点，对于函数 y=f(x) ，使 f(x)=0 的实数 x 叫做函数 y=f(x) 的零点。
-
2.推广:
1）定义|函数：零点是一个函数与x轴的交点（即y=0时的坐标）
2）方程：零点也可以看作是一个方程的解集，即求 f(x) = 0 时 x 的解 -
3.不同图像的零点:
如图:
1）一次函数：y = kx + b ：
当k!=0时，则有一个零点；当k=0时，若y=0则有无数个零点，若y!=0则无零点。2)二次函数：y = ax² + bx + c： 当b² – 4ac > 0 时有两个零点；当 b² – 4ac = 0 时有一个零点；当 b² – 4ac < 0 时没有零点。
3)反比例函数：y = k / x：没有零点。
4)指数函数：y = x ^ k：一个零点。
韩非子·亡征
国小而不处卑，力少而不畏强，无礼而侮大邻，贪愎而拙交者，可亡也。
韩非子·亡征
国小而不处卑位，力弱而不畏强势，没有礼仪而侮辱邻近大国，贪婪固执而不懂外交的，可能灭亡。
是不是国际上有些小国家就是这样的状态。
中国科学技术大学2021年少年班“创新试点班”招生办法（不含上海、浙江）
中国科学技术大学2021年少年班“创新试点班”招生办法（不含上海、浙江）
为进一步深化高等学校招生考试制度改革、加快创新人才选拔培养，根据教育部有关规定，我校在少年班教育改革成果基础上，招收2021年少年班“创新试点班”学生，具体实施办法如下：
继续阅读初中生暑假必读书单
初一年级读书清单
1、《西游记》(吴承恩）
2、《朝花夕拾》(鲁迅)
3、《城南旧事》(林海音)
4、《决战朝鲜》(李峰)
5、《野葫芦引》(宗璞)
6、《飞鸟集》(泰戈尔)
7、《假如给我三天光明》(海伦·凯勒)
初二年级读书清单
1、《水浒传》(施耐庵)
2、《明朝一哥王阳明》(吕峥)
3、《农历》(郭文彬)
4、《1911》(王树增)
5、《中国在梁庄》(梁鸿)
6、《猎杀中国龙》(江涌)
7、《哈姆雷特》、《奥赛罗》、《李尔王》、《麦克白》(莎士比亚)
8、《简爱》(夏洛蒂·勃朗特)
9、《牛虻》(艾捷尔·丽莲·伏尼契)
10、《巴黎圣母院》(雨果)
初三年级读书清单
1、《我与地坛》(史铁生)
2、《林清玄散文》(林清玄)
3、《蒋勋说宋词》(蒋勋)
4、《苏东坡传》(林语堂)
5、《子夜》(茅盾)
6、《陆犯焉识》(严歌苓)
高中生暑假必读书单
根据课标规定：
高中阶段要求学生在课内外加强阅读，培养阅读的兴趣和习惯，提升阅读品味，掌握阅读方法，提高阅读能力，让学生在阅读中拓宽视野，领略人类社会气象与文化，体验中华优秀传统文化、革命文化和社会主义先进文化，提高语言文字运用能力与思想文化修养，丰富精神世界。
下列篇目仅为举例。这些内容，既可以作为“整本书阅读与研讨”“文学阅读与写作”“中国现当代作家作品研习”“中华传统文化经典研习”“外国作家作品研习”等学习任务群的备选，也推荐你们在课外阅读。
继续阅读0812 计算机科学与技术 高校评级
一级学科代码及名称： 0812 计算机科学与技术
本一级学科中，全国具有“博士授权”的高校共 77 所，本次参评75 所；部分具有“硕士授权”的高校 也参加了评估；参评高校共计 238 所（注：评估结果相同的高校排序不分先后，按学校代码排列）。
A+
10001 北京大学
10003 清华大学
10335 浙江大学
90002 国防科技大学
A
10006 北京航空航天大学
10013 北京邮电大学
10213 哈尔滨工业大学
10248 上海交通大学
10284 南京大学
10487 华中科技大学
10614 电子科技大学
A-
10004 北京交通大学
10007 北京理工大学
10145 东北大学
10183 吉林大学
10247 同济大学
10358 中国科学技术大学
10486 武汉大学
10533 中南大学
10698 西安交通大学
10699 西北工业大学
10701 西安电子科技大学
90005 解放军信息工程大学